Formal proofs in propositional logic

When we construct a formal proof in logic we are seeking to show that a certain proposition is derivable from other propositions. We use the words derivation and proof interchangeably.

A sentence \(P\) is derivable in a system of propositional logic from a finite set of sentences if and only if there is a derivation in this system in which all and only the members of the set are primary assumptions and \(P\) is the sentence on the last line.

We express the above symbolically as \(\Gamma \vdash P\) . (Be careful not to confuse derivable (\(\vdash\)) from entails (\(\vDash\)).

Derivability is therefore a property that a proposition can possess relative to a set.

For instance to demonstrate derivability for:

$$ \{ \lnot F \lor D, F, D \rightarrow (G \land H) \} \vdash G \land H $$

We would establish \(\lnot F \lor D, F, D \rightarrow (G \land H)\) as primary assumptions and then, using the derivation rules of the system conclude with \(G\land H\). Every sentence in the derivation is either a primary assumption or an auxiliary assumption or justified by the rules of the derivation.

An auxiliary assumption is an assumption belonging to a sub-derivation. Primary assumptions belong to the main derivation. For any given derivation of the form \(\Gamma \vdash P\) there may be a number of ways of demonstrating the derivation (more than one application of the rules governing the system) but one alone is sufficient to establish derivability.

We will tend to use the terms derivation and proof interchangeably but we should note that there is a technical distinction in that a proof is a derivation in which all of the assumptions have been discharged

Constructing proofs

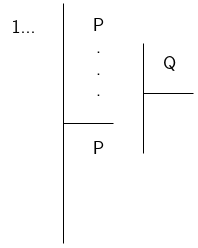
We place assumptions above derivations and mark them A in the right-hand margin. We use a shorthand for the derivation rules and also place these in the right-hand margin.

We divide assumptions from derivations with a horizontal line. We number each line and use this to refer to the line we are applying the derivation to. Sub-proofs follow this structure recursively. This is known as Fitch notation

Schematically:

Applied example:

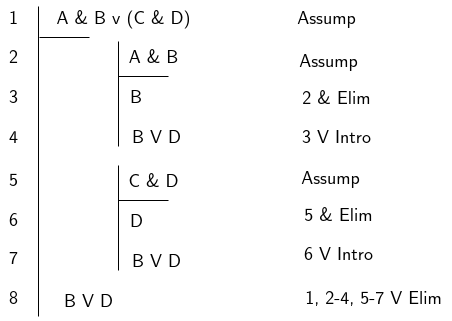
Sub-proofs

When a sub-proof is terminated, the assumption with which it starts is said to be discharged. It’s conclusion can then be drawn upon and invoked within the main proof by reference to its start and end line number. However statements within the sub-proof cannot be referred to again from within the main proof, only its result.

Derivation rules

Derivation rules are Syntax_of_sentential_logic rather than semantic. They are applied on the basis of their form rather than on the basis of the truth conditions of the sentences they are applied to.

Derivation rules can be applied without having an interpretation of the symbols in mind. A derivation rule tells us that: given a group of symbols with a certain structure, we can write down another group of symbols with a certain structure.

Each of the main logical connectives has an associated derivation rule. The binary connectives have pairs of rules, one for the introduction of the connective and one for its elimination.

The main derivation rules:

• Negation Introduction
• Negation Elimination
• Conjunction Introduction
• Conjunction Elimination
• Disjunction Introduction
• Disjunction Elimination
• Conditional Introduction
• Disjunction Elimination
• Biconditional Introduction
• Biconditional Elimination