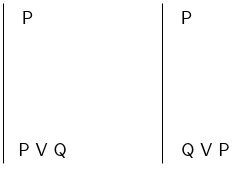Disjunction Introduction

This rule can seem a little odd: like we are randomly introducing an additional proposition without giving any justification. However this is just a consequence of the fact if \(P\) is true, so is \(P \lor Q\) since disjunction is not the same as conjunction: only one disjunct needs to be true for the compound disjunction to be true. This is represented in the context of truth-trees by the fact that truth can pass up via either branch of a disjunction pattern. This rule is sometimes also referred to (confusingly) as Addition.