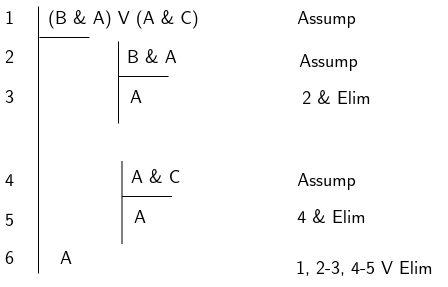
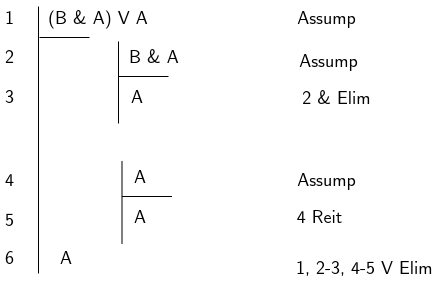
Disjunction Elimination
This rule is sometimes also referred to as Constructive Dilemma. This can be a bit tricky to understand because the goal is to derive or introduce a new proposition separate from the disjunction you start out with. This may be disjunction, a single proposition or a proposition containing any other logical connective. You do this by constructing two sub-proofs, one for each of the disjuncts comprising the disjunction you start out with. If you can derive your target proposition as the conclusion of each subproof then you may invoke the conclusion in the main proof and take it to be derived.
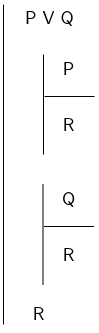
Here is an example where Disjunction Elimination is used to derive a new disjunction.
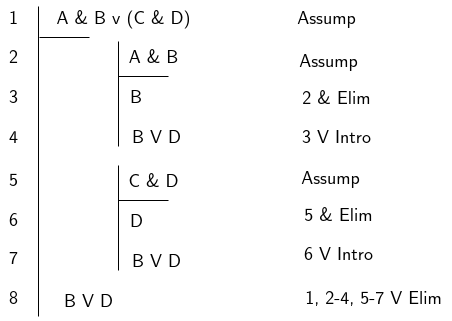
Here are two further examples that use Disjunction Elimination to derive singular propositions