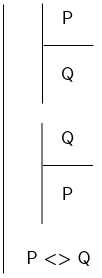
Biconditional introduction

The biconditional means if $P$ is the case, $Q$ must be the case and if $Q$ is the case, $P$ must be the case. Thus to introduce this operator we must demonstrate both that $Q$ follows from $P$ and that $P$ follows from $Q$. We do this via two sub-proofs.