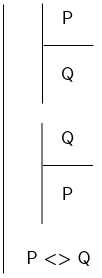
Logical equivalence
Two sentences, P and Q, are truth-functionally equivalent if and only if there is no truth assignment in which P is true and Q is false
Informal expression
P: If it is raining then the pavement will be wet.
Q: The pavement is not wet unless it is raining.
Formal expression
$$ (P \rightarrow Q) \longleftrightarrow (\lnot P \lor Q) $$
Truth-tables
| \(P\) | \(Q\) | $ P \rightarrow Q $ | $ \lnot P \lor Q$ |
|---|---|---|---|
| T | T | T | T |
| T | F | T | F |
| F | T | T | T |
| F | F | F | T |
Derivation
Propositions \(P\) and \(Q\) are equivalent in a system of derivation for propositional logic if \(Q\) is derivable from \(P\) and \(P\) is derivable from \(Q\).
Note that the property of equivalence stated in terms of derivablity above is identical to the derivation rule for the material biconditional: