Voltage
Difference of potential and the transfer of energy
We noted in the discussion of current that current flows when there is a difference of potential between two points with negatively charged atoms at one point and positively charged atoms at the other.
Difference of potential is the same thing as voltage. Voltage is essential to current because it is the force that enables the current to flow.
Without voltage there can be no current because in their natural state, the electrons in an atom are in random motion with no direction. To produce a current, energy must be imparted to the electrons so that they all flow in the same direction.
Voltage is the application of this energy. Any form of energy that dislodges electrons from atoms can be used to produce current. Thus:
Voltage is the work required per coulomb to move a charge from one point to another.
Voltage exists even without current
Given that voltage is the force that generates current, it would be natural to think that voltage only exists when a voltage source (such as a battery) is connected to a circuit. This however is not the case. Even if a 9V battery isn’t connected to anything it still has a difference of potential of 9-volts accross its terminals. Remember voltage is potential energy not just the actualisation of that energy.
Voltage rise and voltage drops
In circuits there are actually two types of voltage:
- Voltage rise
- Voltage drop
Voltage rise
When we introduce potential energy into a ciruit in the form of voltage, this is a voltage rise. The current flows from the negative terminal of the voltage source and returns to the positive terminal of the voltage source.
A 12V battery connected to a circuit gives it a voltage rise of 12 volts.
Voltage drop
Voltage drop is the corrolary to voltage rise. It is the loss of energy that the electrons of the circuit current experience as a result of encountering resistance.
As they move through the circuit the electrons encounter a load which is what we call resistance to the flow of current. As they run into this, they give up their energy. The relinquishing of energy happens in the form of a conversion of electrical energy to heat (hence why computers heat up). The amount lost is equal to the amount of energy imparted by the voltage rise.
The voltage drop in a circuit equals the the voltage rise of the circuit because energy cannot be created or destroyed, only changed to another form. When a voltage rise is converted to a voltage drop we say that the energy has been consumed by the circuit.
Examples
- If a 12V source is connected to a 12V lamp, the source supplies a 12V voltage rise and the lamp produces a 12V voltage drop.
- If two identical 6V lamps are connected in series to the same 12V source, each lamp produces a 6V drop for a total of 12 volts
- If two different lamps are connected in series to to a 12V source: a 3V and a 9V lamp, the 9V lamp produces a drop of 9V and the 3V lamp produces a drop of 3V. The sum of the voltage drops equals the voltage rise of 12 volts.
These examples demonstrate that the voltage rise: voltage drop ratio always evens out.
Kirchoff’s Voltage Law
The relationship between voltage rise and voltage drop is expressed in Kirchoff’s Voltage Law:
The sum of the voltages around any closed loop in a circuit must be zero.
The application of the Law is illustrated in the following diagram:
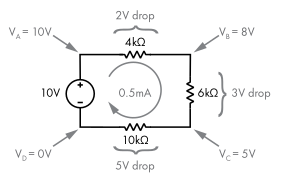
The explanation for the voltage drop at the positions \(V^{A}\) and \(V^{D}\) are obvious enough: they are at the beginning and end of the loop so are equal to the maximal voltage rise and minimal voltage drop, respectively.
We can work out the voltage of the remaining voltage points by inverting Ohm’s Law: \(V = I \times R\):
For the voltage at \(V^{B}\):
$$ 0.5\textsf{mA} \times \textsf{4}k\Omega = 2 \textsf{V} $$
For the voltage at \(V^{C}\):
$$ 0.5\textsf{mA} \times \textsf{6}k\Omega = 3 \textsf{V} $$
The total drops (2V, 3V, 5V) are equal to the initial volatage rise (10V)
Distinguishing voltage from electric field
It can be confusing that two different symbols often seemed to be used interchangeably when talking about voltage: \(V\) and \(E\). However, while they broadly point to the same phenomenon there is a difference in emphasis.
- \(V\) stands for volts or voltage conceived purely in terms of the difference in potential between two points: the positive and negative terminals
- \(E\) stands for electric field. This is the field that surround each electric charge and exerts force on all other charges in the field, attracting or repelling them. So it is more the physical process that the volatage represents rather than the numerical representation of the potential between the terminals.