Two’s complement
Summary
Two’s complement is a method for representing signed numbers (negative integers) in binary.
It is derived by inverting the values of an unsigned binary integer to create its signed equivalent.
A benefit is that hardware implementation of the binary arithmetic of signed and unsigned numbers can be handled in the same manner as unsigned numbers, requiring no additional handling. A drawback is that it halves the informational capacity of the given word length for the binary system.
Detail
Procedural steps
Two’s complement divides the available word length (see binary encoding) into two subsets: one for negative integrs and one for positive integers.
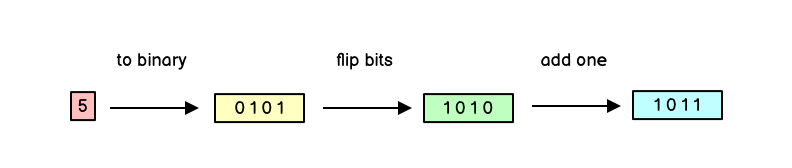
Take the binary encoding of decimal five (0101). Its complement is 1011.
The procedure for deriving the complement is as follows.
To derive the complement of an unsigned number:
- Take the unsigned number and invert its digits:
0becomes1,1becomes0 - Add one
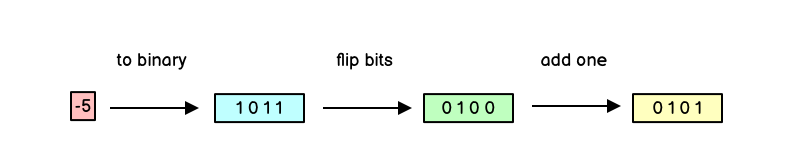
To derive the unsigned equivalent of a signed number you invert the process but still make the smallest digit 1:
Formal expression
$$ 2^n - x $$
- where \(x\) is the negative integer in binary that we wish to derive
- where \(n\) is the word length of the binary system in bits.
Applied to the earlier example we have \(2^4 -5\) which is:
$$ 16 - 5 = 11 $$
When we convert the decimal 11 to binary we get 1011 which is identical to the signed version of the unsigned integer.
We can confirm the correctness of the derviation by summing the signed and unsigned binary values. If this results in zeros (ignoring the overflow bit), the derivation is correct as the two values effectively cancel each other out:
$$
1011 + 0101 = 0000 $$
Advantages
- The circuit implementation of arithmetic involving positive and negative integers is the same as the implementation of positive integers. There is no need for additional harware or special handling of the values.
- This can be contrasted with the alternative approaches to signing numbers such as signed magnitude representation which uses certain bits as designators of negative/positive status.
Limitations
Two’s complement reduces the overall informational capacity of the given binary word length, effectively halving the total number of unique values.
In a 4-bit system instead of 16 total unique encodings of integers you have 8 encodings for positive integers and 8 encodings for the their signed equivalent. For integers larger than denary 8 you would need to increase the bit length of the system
Consequently two’s complement can necessitate larger overall word lengths.
Related notes
signed_and_unsigned_numbers, binary addition, Signed magnitude representation