Reducing fractions to their lowest terms
A fraction is said to be reduced to its lowest terms if the greatest common divisor of the numerator and the denominator is $1$.
Whenever we reduce a fraction, the resultant fraction will always be equivalent to the fraction we started with.
Thus the fraction \(\frac{2}{3}\) is reduced to its lowest terms because the greatest common divisor is 1. Neither the numerator or the denominator can be reduced to any lower terms. In contrast, the fraction \(\frac{4}{6}\) is not reduced to its lowest terms because the greatest common divisor of both 4 and 6 is 2, not 1.
1. Reducing with repeated application of divisors
The following demonstrates the process of reducing a fraction to its lowest terms in a series of steps:
$$ \\frac{18}{24} = \frac{18/2}{24/2} = \frac{9}{12} = \frac{9/3}{12/3} = \frac{3}{4} $$
_Once we get to \(\frac{3}{4}\) the greatest common divisor is 1, therefore \(\frac{18}{24}\) has been reduced to its lowest terms _.
2. Reducing in one step with the highest common divisor
In the previous example the reduction took two steps: first we divided by two and then we divided by three. There is a more efficient way: find the highest common divisor of the numerator and denominator and then use this as the basis for the reduction. With this method, the reduction can be completed in a single step.
The greatest common divisor of 18 and 24 is 6, thus:
$$ \frac{18}{24} = \frac{18/6}{24/6} = \frac{3}{4} $$
Note how our earlier two divisors 2 and 3 are factors of 6, showing the consistency between the two methods.
3. Reducing with factors and cancellation
The two methods above are not very systematic and are quite heuristic. The third approach is more systematic and relies on the interchangeability of factors and divisors.
Instead of thinking asking what is the greatest common divisor of 18 and 24 we could ask: which single number can we multiply by to get 18 and 24? Obviously both numbers are in the six times table. This is therefore to say that 6 is a factor of both: we can multiply some number by 6 to arrive at both 18 and 24. The numbers are 3 and 4 respectively:
$$ \\begin{split} 3 \cdot 6 = 18 \\ 4 \cdot 6 = 24 \\end{split} $$
Here, 3 and 4 are the multiplicands of the factor 6. As \(\frac{3}{4}\) doesn’t have a lower common factor, it is therefore defined in its lowest terms.
Once we have reached this point, we no longer need the common factor 6, we can therefore cancel it out, leaving the multiplicands as the reduced fraction:
$$ \\begin{split} 3 \cancel{\cdot6= 18}\\ 4 \cancel{\cdot6= 24} \\end{split} $$
4. Reducing with prime factorisation
This is still a bit long-winded however particularly when finding the factors of larger numbers because we have to go through the factors of both numbers to find the largest held in common.
A better method is to utilise prime factorization combined with the canceling technique.
First we find the prime factors of both the numerator and denominator: 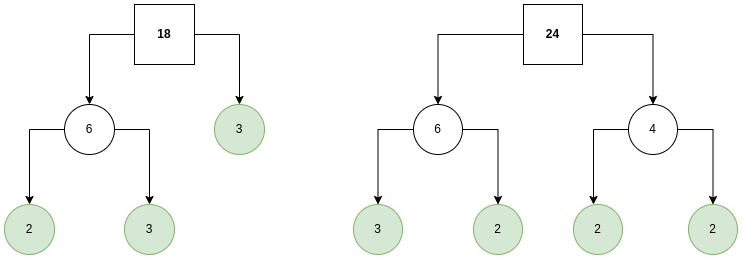
This gives us:
$$ \\frac{18}{24} = \frac{2 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3} $$
We then cancel out the factors held in common between the numerator and denominator:
$$ \\frac{\cancel{2} \cdot \cancel{3} \cdot 3}{\cancel{2} \cdot 2 \cdot 2 \cdot \cancel{3}} $$
This gives us:
$$ \\frac{3}{2 \cdot 2} $$
We then simplify the fraction as normal to its lowest term (conducting any multiplications required by what is left from the prime factorization):
$$ \\frac{3}{4} $$
Reducing fractions that contain variables
Superficially this looks to be more difficult but in fact we can apply the same prime factorization method to get the result.
Demonstration
Reduce the following fraction to its lowest terms: $$\frac{25a^3b}{40a^2b^3}$$
The prime factors of the numerator and denominator:
$$ \\begin{split} 25 = {5, 5} \\ 40 = {2,2,2,5} \\end{split} $$
Now we apply canceling but we include the variable parts, treating them exactly the same as the coefficients. We break them out of their exponents however.
$$\frac{25a^3b}{40a^2b^3} =\frac{5 \cdot 5 \cdot a \cdot a \cdot a \cdot b}{2 \cdot 2 \cdot 2 \cdot 5 \cdot a \cdot a \cdot b \cdot b \cdot b }$$
Canceled:
$$\frac{\cancel{5} \cdot 5 \cdot \cancel{a} \cdot \cancel{a} \cdot a \cdot \cancel{b}}{2 \cdot 2 \cdot 2 \cdot \cancel{5} \cdot \cancel{a} \cdot \cancel{a} \cdot \cancel{b} \cdot b \cdot b }$$
Which gives us:
$$ \\frac{5 \cdot a}{2 \cdot 2 \cdot 2 \cdot b \cdot b} = \frac{5a}{8b^2} $$
Reducing fractions that contain negative values
Reduce the following fraction to its lowest terms: $$\frac{14y^5}{-35y^3}$$
This fraction is an instance of a fraction with unlike terms.
Apply Prime factorization:
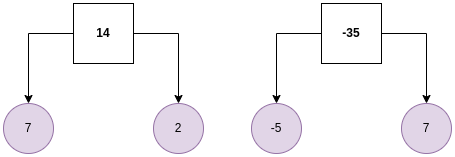
Cancel the coefficients and variable parts
$$ \\frac{14y^5}{-35y^3}=\frac{5 \cdot 7 \cdot 2 \cdot y \cdot y \cdot y \cdot y \cdot y}{-5 \cdot 7 \cdot y \cdot y \cdot y} = - \frac{2y^2}{5} $$
Reduce the following fraction to its lowest terms: $$\frac{- 12xy^2}{ - 18xy^2}$$
This fraction is an instance of a fraction with like terms.
Apply Prime factorization:

Cancel the coefficients and variable parts
$$
- \frac{12xy^2}{18xy^2}=\frac{3 \cdot 2 \cdot 2 \cdot x \cdot y \cdot y}{3 \cdot 7 \cdot 3 \cdot 2 \cdot x \cdot x \cdot y} = - \frac{2y}{3x} $$