Logical consistency
Informal definition
A set of propositions is consistent if and only if it is possible for all the members of the set to be true at the same time. A set of propositions is inconsistent if and only if it is not consistent.
Demonstration
The following set of propositions form an inconsistent set:
- Anyone who takes astrology seriously is a lunatic.
- Alice is my sister and no sister of mine has a lunatic for a husband.
- David is Alice’s husband and he read’s the horoscope column every morning.
- Anyone who reads the horoscope column every morning takes astrology seriously.
The set is inconsistent because not all of them can be true. If (1), (3), (4) are true, (2) cannot be. If (2), (3),(4) are true, (1) cannot be.
Formal definition
A finite set of propositions \(\Gamma\) is truth-functionally consistent if and only if there is at least one truth-assignment in which all propositions of \(\Gamma\) are true.
Informal expression
The book is blue or the book is brown
The book is brownFormal expression
$$ \{P \lor Q, Q\} $$
Truth table
$ {P, Q} $ form a consistent set because there is at least one assignment when both propositions are true. In fact there are two (corresponding to each disjunct) but one is sufficient.
| \(P\) | \(Q\) | $ P \lor Q $ | \(Q\) |
|---|---|---|---|
| T | T | T | T |
| T | F | T | F |
| F | T | T | T |
| F | F | F | F |
Derivation
In terms of logical derivation, a finite \(\Gamma\) of propositions is inconsistent in a system of derivation for propositional logic if and only if a proposition of the form \(P \& \lnot P\) is derivable from \(\Gamma\). It is consistent just if this is not the case.
In other terms, if you can derive a contradiction from the set, the set is logically inconsistent.
A contradiction has very important consequences for reasoning because if a set of propositions is inconsistent, any other proposition is derivable from it.
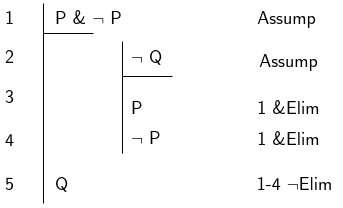
A demonstration of the the consequences of deriving a contradiction in a sequence of reasoning.
Here we want to derive some proposition \(Q\). If we can derive a contradiction from its negation as an assumption then, by the negation elimination) rule, we can assert \(Q\). This is why contradictions should be avoided in arguments, they ‘prove’ everything which, by association, undermines any particular premise you are trying to assert.