Recursion
A recursive function is a function that calls itself in its definition.
More generally recursion means when a thing is defined in terms of itself. There are visual analogues that help to represent the idea such as the Droste effect where an image contains a version of itself within itself. The ouroboros is another example. Also fractals display recursive properties.
Schema
The general structure of a recursive function is as follows: 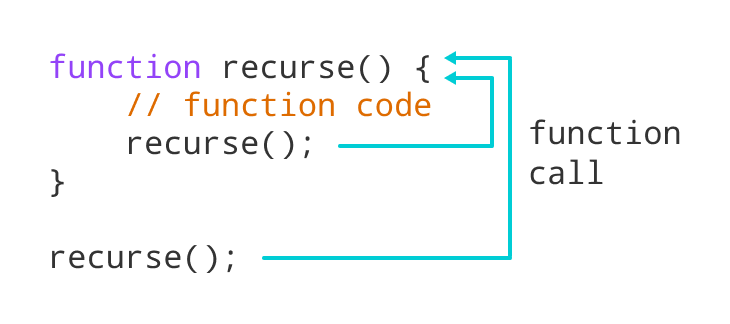
Why use recursive functions?
Recursion is made for solving problems that can be broken down into smaller, repetitive problems. It is especially good for working on things that have many possible branches but are too complex for an iterative approach or too costly in terms of memory and time complexity.
Recursive programming differs from iterative programming but both have similar use cases. Looping is a canonical example of working iteratively.
Base condition
Once a condition is met, the function stops calling itself. This is called a base condition.
Because recursion has the potential for infinity, to use it, we must specify a point at which it ends. However as we are not using an iterative approach we cannot rely on while or foreach to specify the boundaries of its operation. We call this the base condition and this will typically be specified using conditional logic.
The schema for a recursive function with a base condition is:
function recurse() {
if (condition) {
recurse();
} else {
// stop calling recurse()
}
}
recurse();Demonstrations
Countdown
// program to count down numbers to 1
function countDown(number) {
// display the number
console.log(number);
// decrease the number value
let newNumber = number - 1;
// base case
if (newNumber > 0) {
countDown(newNumber);
}
}
countDown(4);- This code takes
4as it’s input and then outputs a countdown returning:4, 3, 2, 1 - In each iteration, the number value is decreased by 1
- The base condition is
newNumber > 0. This breaks the recursive loop once the output reaches1and stops it continuing into negative integers.
Each stage in the process is noted below:
countDown(4) prints 4 and calls countDown(3)
countDown(3) prints 3 and calls countDown(2)
countDown(2) prints 2 and calls countDown(1)
countDown(1) prints 1 and calls countDown(0)Finding factorials
The factorial of a positive integer n is the product of all the positive integers less than or equal to n.
To arrive at the factorial of n you subtract 1 from n and multiply the result of the subtraction by n. You repeat until the subtractive process runs out of positive integers. For example, if 4 is n, the factorial of n is 24:
$$ 4 _ 3 _ 2 \*1 $$
4 multiplied by 3 gives you 12, 12 multiplied by 2 gives you 24. 24 multiplied by 1 is 24.
This is clearly a process that could be implemented with a recursive function:
// program to find the factorial of a number
function factorial(x) {
// if number is 0
if (x === 0) {
return 1;
}
// if number is positive
else {
return x * factorial(x - 1);
}
}
let num = 3;
// calling factorial() if num is non-negative
if (num > 0) {
let result = factorial(num);
console.log(`The factorial of ${num} is ${result}`);
}