3-bit Counter

To demonstrate the use of Flip-Flops we will create the circuit for a 3-bit counter. This simply counts up from 0 to 7 because 7 is the maximum decimal number we can create with three bits (\(2^3\)):

Binary	Decimal
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

The circuit will have three memory components, each representing one bit of the 3-bit number. When the clock pulses, the 3-bit number increments by one. We need to synchronise the operation with a clock because each bit by itself is meaningless, it only gains meaning by the relation it sustains to the other two bits hence it must be kept in sync with them.

We can derive the circuit arrangement by analysing the outputs of a flipflop at each pulse:

Combined bits	Q2	Q1	Q0	Decimal
000	0	0	0	0
001	0	0	1	1
010	0	1	0	2
011	0	1	1	3
100	1	0	0	4
101	1	0	1	5
110	1	1	0	6
111	1	1	1	7

If we look at the pattern of each flip-flops’ output we notice the following:

• Q0 toggles on every pulse
• Q1 toggles every time Q0 was previously 1
• Q2 toggles when both Q1 and Q0 were previously 1

This means that to construct a circuit that displays this behaviour we just have to use a T flip-flop since the only state change we need is a single bit toggle three times that retains its value.

Using these pulse patterns we can construct a circuit as follows: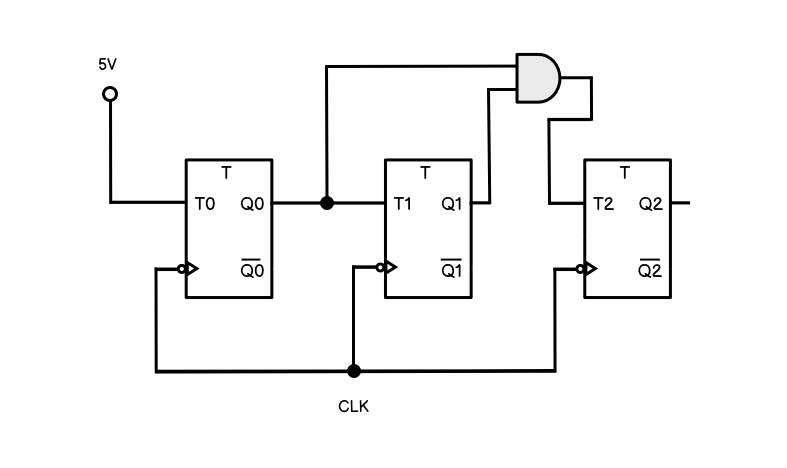

Remember from the table: Q2 is the most significant bit and Q0 is the least significant bit so we should read the output in the interactive circuit backwards, reversing the order. Then we will see that the cicuit is cyling through 0-7

This is how the circuit works:

• All three flip-flops are connected to the same clock signal so that they are synchnonised
• Because T0 is connected to the voltage source Q0 toggles every time the clock pulses
• T1 is connected to Q0 so a clock pulse causes Q1 to toggle only when Q0 is high in line with the table
• T2 is connected to Q0 AND Q1 so Q2 only toggles on a clock pulse when Q0 and Q1 are both high