Theorems and empty sets
We know that when we construct a derivation we start from a set of assumptions and then attempt to reach a proposition that is a consequence of the starting assumptions. However it does not always have to be the case that the starting set contains members. The set can in fact be empty.
Demonstration
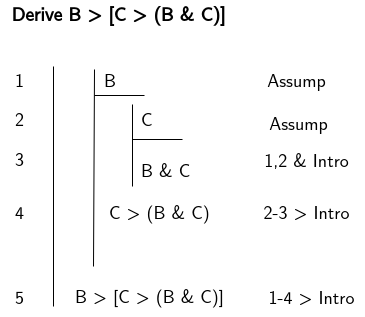
We see in this example that there is no starting set and thus no primary assumptions. Instead we start with nothing other than the proposition we wish to derive. The proposition is effectively derived from itself. In these scenarios we say that we are constructing a derivation from an empty set.
Propositions which possess this property are called theorems:
A proposition \(P\) or a system of propositions in propositional logic is a theorem in a system of derivation for that logic if \(P\) is derivable from the empty set.
We represent a theorem as:
$$ \vdash P $$
(There is no preceding \(\Gamma\) as the set is empty. )